Effortless Simplex Grid
Background
Recently at work, I needed to draw an infinite simplex grid in the fragment shader to prototype height shading and contours of Digital Terrain Models in shadertoy. While searching for an efficient approach I stumbled upon this lovely shader by Shane. First I was very confused by the values and magic numbers used to do that in the shadertoy. But, with a little help from my good friend ChatGPT, I realized that the values originate from the Simplex noise algorithm—a technique devised by Ken Perlin in 2001. The transformation squashes a uniform grid in a way that forms equilateral triangles.
Now, if you know me, you know that I can’t just use something without mathematically proving why it works or at least gain a deeper intuition of why it works. So the focus of this post is to derive this 2D transformation.
But first, let’s build some intuition
Intuition
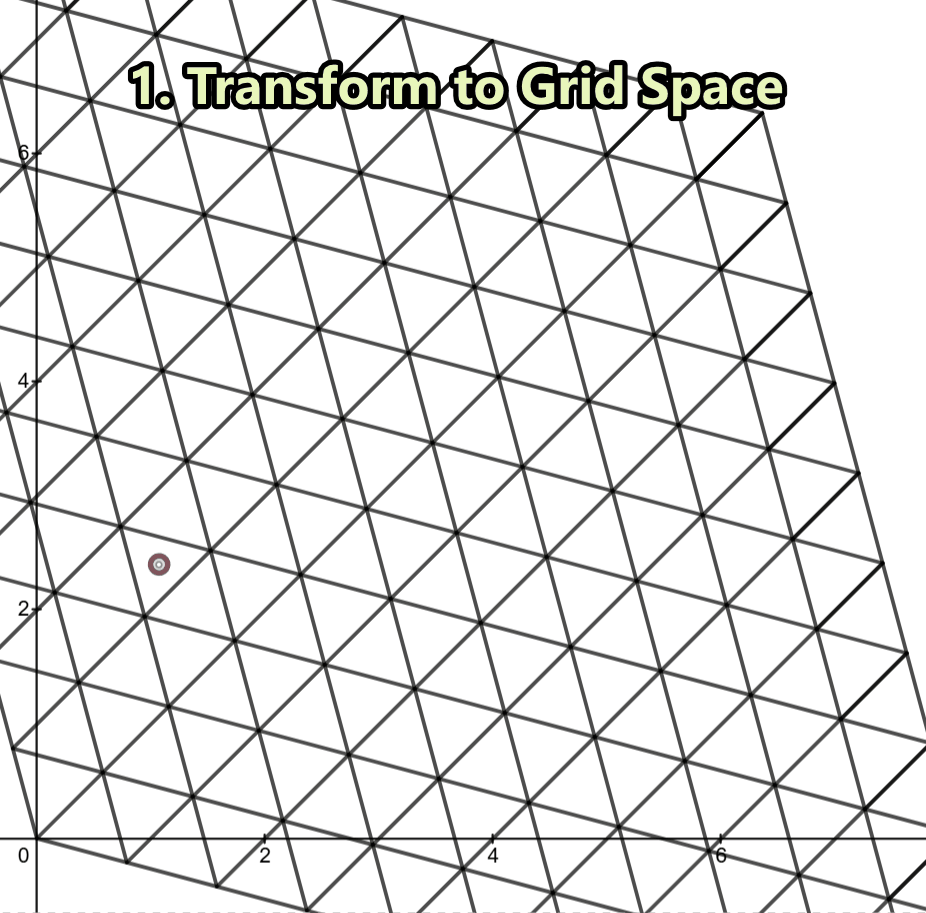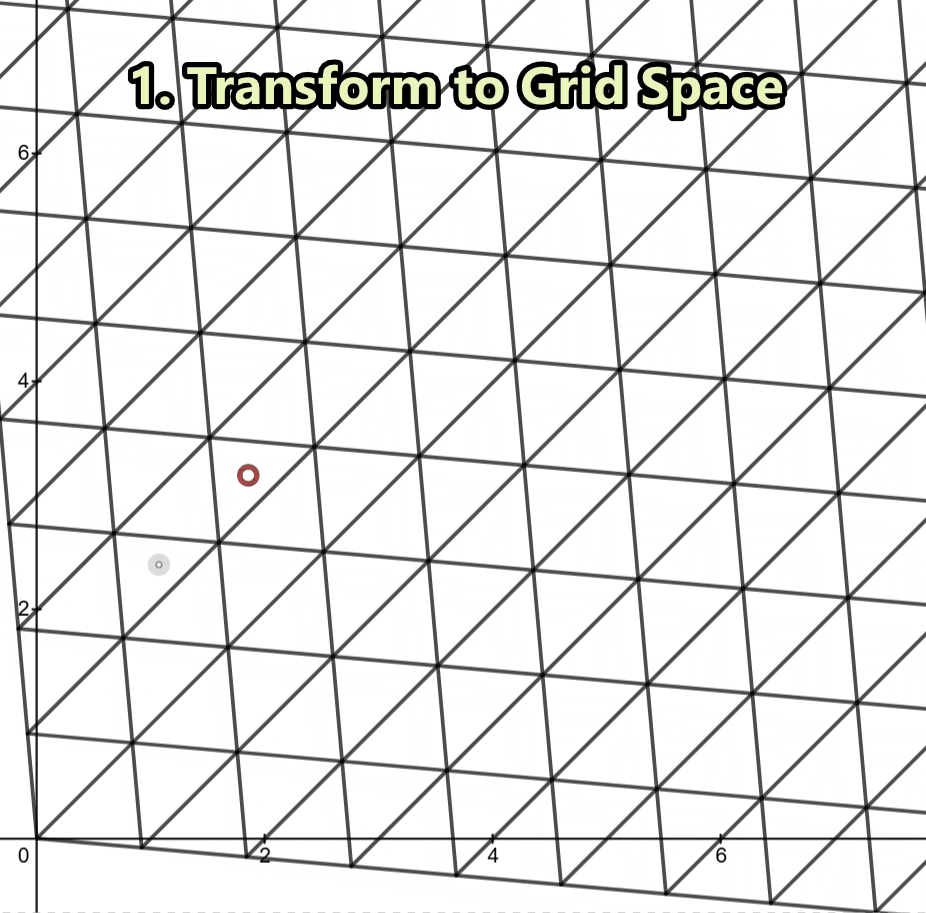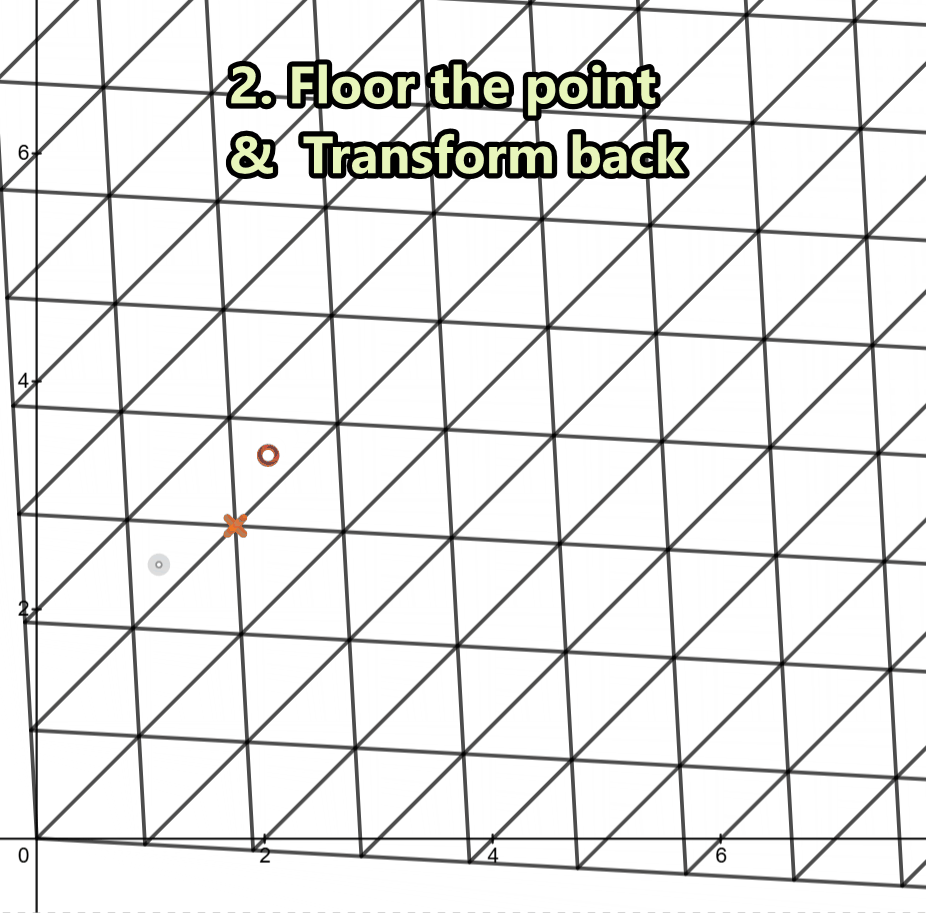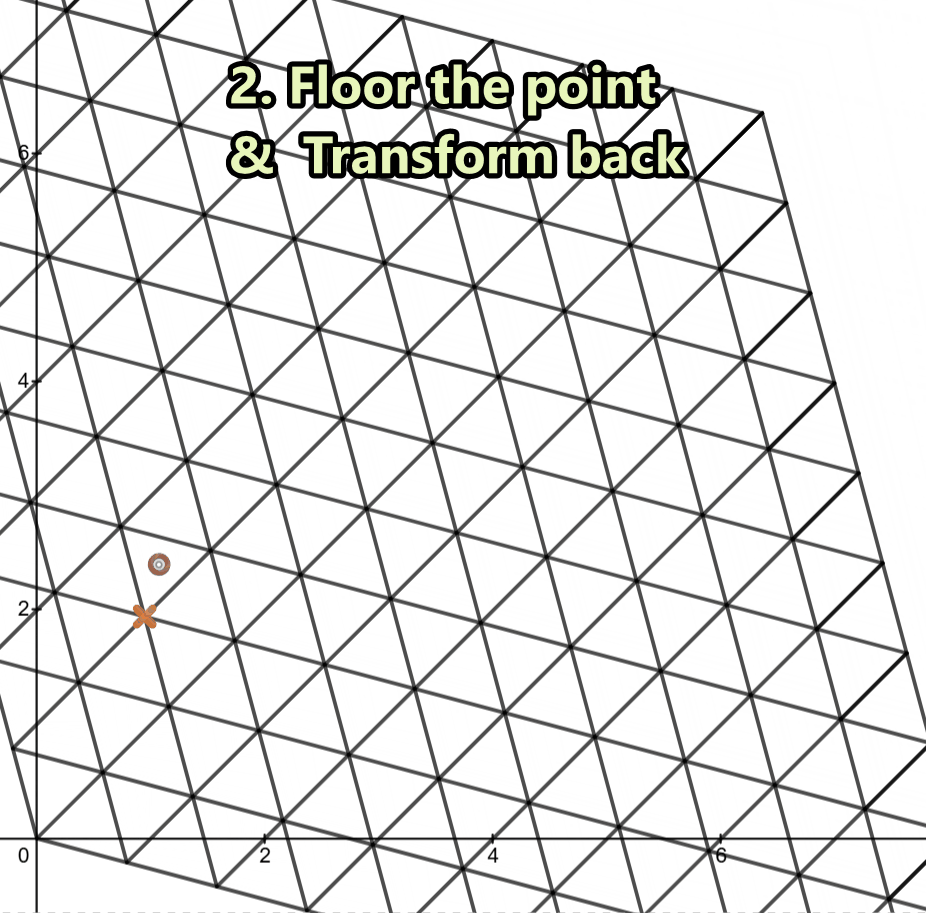
In order to draw a equilateral triangle grid we need to first figure out the triangle our point p resides in, and then retrieve it’s vertices. So how do we do that?
In a uniform grid, if we want to determine which square cell a point belongs to, we simply take floor(x) and floor(y), which gives us the coordinates of the bottom-left corner of the cell. Makes us wonder—can we do something similar for an equilateral triangle grid?
If only we could just floor() our point and instantly get the nearest triangle corner! Unfortunately, life isn’t that simple… or is it?
This is exactly where the simplex transformation comes in. We stretch and shear our space so that the equilateral triangles lie perfectly with the square grids. Now in this transform space we simple floor() our point in question to snap it to the closest grid corner—just like we would in a uniform grid.
We then transform that snapped corner back into our original space where it now represents the triangle corner.
So Effortless and Efficient!
Derivation of this transformation
Now, let’s derive this transformation based on assumptions on how it should behave:
Observation 1: Linearity and Matrix Representation
The transformation preserves straight lines and maintains parallelism without translation, it must be a linear transformation.
It is a linear transformation in 2D, so it can be represented by a 2×2 matrix:
\[\begin{bmatrix} a & b \\ c & d \end{bmatrix}\]Observation 2: It is a symmetric transformation!
We’re squashing perperndicular to the $x=y$ diagonal. This is a shear along diagonal where:
- Points on the x=y line stay on the $x=y$ line.
- Lines perpendicular to x=y, stay perperndicular to x=y line (and Points on the $x=-y$ line stay on the $x=-y$ line)
Based on the facts above we can deduce that the transformation is a symmetrical one!
\[\begin{bmatrix} a & b \\ b & a \end{bmatrix}\]Observation 3: Lines parallel to the x=y will not be affected by the transformation
We’re squashing perperndicular to the x=y diagonal, any line parallel to it will remain on it’s position.
for example let’s see how $y=x+1$ is affected:
\[\begin{bmatrix} a & b \\ b & a \end{bmatrix} \begin{bmatrix} x \\ x+1 \end{bmatrix} = \begin{bmatrix} ax + b(x+1) \\ bx + a(x+1) \end{bmatrix}\]the result still should be on the $y=x+1$ line, For this to hold true we must have $a=b+1$
The matrix transformation now has reduced to this:
\[\begin{bmatrix} b+1 & b \\ b & b+1 \end{bmatrix}\]Deriving the value
Based on the constraints and observations above we have discovered that the whole 2x2 linear transformation depends on a single value. see how changing this value will affect the transformation.
Now, we need to find the value that will transform uniform grids in such a way that the grid sides and diagonal form equilateral triangles after transformation. In other words, we need to find the value of $b$ for which the diagonal of the grid cell will have the same length as its sides.
To put it another way: find for what value of $b$, length of the transformed $(1, 0)$ will be equal to transformed $(1, 1)$
- Transforming $ (1, 1) $
- Transforming $ (0, 1) $
We want these two to have the same length, we solve for $b$ in the equation below:
\[\sqrt{(2b+1)^2 + (2b+1)^2} = \sqrt{b^2 + (b+1)^2}\]One of the two solutions to this is:
\[\frac{\sqrt{3}-3}{6}\]The other solution mirrors the grid.
We have found the value used to transform a grid!
Here is the final transformation used to get the uniform grid into simplex space:
\[\begin{bmatrix} \frac{\sqrt{3}-3}{6} + 1 & \frac{\sqrt{3}-3}{6} \\ \frac{\sqrt{3}-3}{6} & \frac{\sqrt{3}-3}{6} + 1 \end{bmatrix}\]I trust the reader can find the inverse of this transformation very easily :)
Final words
Similar intuition and arguments work for the 3D version of the algorithm which I didn’t have much chance to get into.
Additionaly I would like to note that the derivation is something I worked through based on my existing knowledge. If you know a simpler or more intuitive way to arrive at the final transformation matrix, I’d love to hear it!
I hope you have found this blog post useful. I’ve tried, in my own way, to show how some problems can be solved in a simple way. If you’ve found any errors in my logic or math, please contact me.